The aim of this tutorial is to introduce the use of VES for obtaining kinetic information of activated processes. We will learn how to set up a biased simulation using a fixed flooding potential acting on a relevant slow degree of freedom. We can then scale the accelerated MD time in a post-processing procedure.
Once this tutorial is completed students will:
The tarball for this project contains the following files:
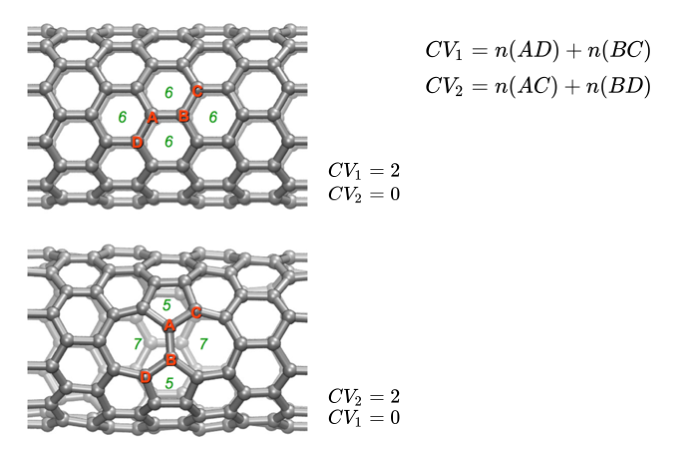
As an example of an activated process in materials science, we will work with the Stone-Wales transformation in a carbon nanotube. The tarball for this project contains the inputs necessary to run a simulation in LAMMPS for a 480 atom carbon nanotube. We use the AIREBO (Adaptive Intermolecular Reactive Empirical Bond Order) force field parameters which can approximately describe C-C bond breakage and formation at reasonable computational cost. For CVs we can use the coordination number in PLUMED to measure the number of covalent bonds among different groups of atoms. The transformation involves breaking two C-C bonds and forming two alternative C-C bonds.A definition of these CVs as well as the relevant C-C bonds are depicted in Figure stone-wales. We prepare a PLUMED input file as follows.
# set distance units to angstrom, time to ps, and energy to eV UNITS LENGTH=A TIME=ps ENERGY=eV # define two variables COORDINATION GROUPA=229,219 GROUPB=238,207 R_0=1.8 NN=8 MM=16 PAIR LABEL=CV1 COORDINATION GROUPA=229,219 GROUPB=207,238 R_0=1.8 NN=8 MM=16 PAIR LABEL=CV2 # the difference between variables COMBINE ARG=CV1,CV2 COEFFICIENTS=1,-1 POWERS=1,1 LABEL=d1 PERIODIC=NO
In the above, the first line sets the energy units. The second and third line define the two CVs for the C-C covalent bonds. (We have chosen atoms 238,207,229 and 219; however this choice is arbitrary and other atoms could equally well have been chosen.) Lastly, we define a simple approximate reaction coordinate given by the difference between CV1 and CV2 that we can use to monitor the transition.
Next we will use VES to drive the transformation at 1700 K. We bias the formation of bonds DB and AC shown in Figure stone-wales using CV2 which changes from 0 to 2 during the transformation. (Although a more rigorous treatment would bias both CVs, for this tutorial we will simplify things and work in only one dimension). We choose a Chebyshev polynomial basis set up to order 36
# The basis set to use bf1: BF_CHEBYSHEV ORDER=36 MINIMUM=0.0 MAXIMUM=2.0
and we tell PLUMED to use VES acting on CV2 with a free energy cutoff
td_uniform: TD_UNIFORM VES_LINEAR_EXPANSION ... ARG=CV2 BASIS_FUNCTIONS=bf1 LABEL=variational TEMP=1700 BIAS_CUTOFF=15.0 BIAS_CUTOFF_FERMI_LAMBDA=10.0 TARGET_DISTRIBUTION=td_uniform ... VES_LINEAR_EXPANSION
Here we are biasing CV2 with the basis set defined above. The final two lines impose the cutoff at 15 eV. The cutoff is of the form
\[ \frac{1}{1+e^{\lambda [F(s)-F_c]}} \]
where \(\lambda\) (inverse energy units) controls how sharply the function goes to zero. Above we have set \(\lambda=10.0\) to ensure the cutoff goes sharply enough to zero.
The following input updates the VES bias every 200 steps, writing out the bias every 10 iterations. To enforce the energy cutoff we also need to update the target distribution which we do every 40 iterations with the TARGETDIST_STRIDE flag.
OPT_AVERAGED_SGD ... BIAS=variational STRIDE=200 LABEL=var-S STEPSIZE=0.1 COEFFS_FILE=coeffs.dat BIAS_OUTPUT=10 TARGETDIST_STRIDE=40 TARGETDIST_OUTPUT=40 COEFFS_OUTPUT=1 ... OPT_AVERAGED_SGD
Finally, we will stop the simulation when the transition occurs using the COMMITTOR in PLUMED
COMMITTOR ARG=d1 BASIN_LL1=-2.0 BASIN_UL1=-1.0 STRIDE=600
Run the simulation using LAMMPS
lmp_mpi < input
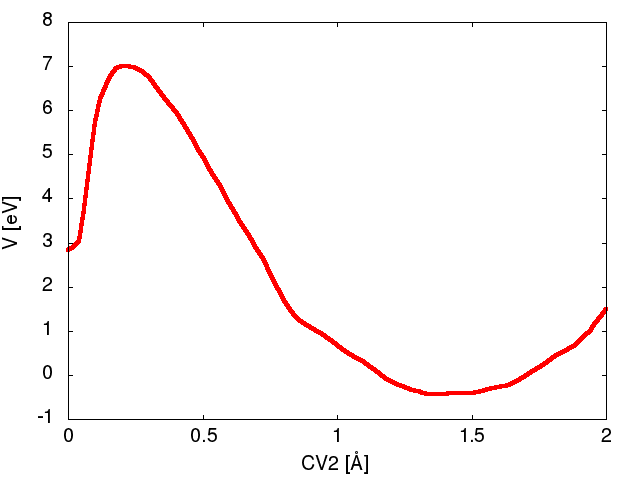
and plot the last few bias output files (bias.variational.iter-n.data) using gnuplot. What is the difference between the maximum and minimum values of the bias obtained during the simulation? Is the cutoff value sufficient to cross the barrier? Is the cutoff value too large?
Figure Figure1A shows an example bias potential after 90 iterations. Note that a cutoff of 15 eV is too large as the system transitions before the bias reaches the prescribed cutoff. From Figure Figure1A we see a barrier height of approximately 7.3 eV.
The output also produces an movie.xyz file which can be viewed in vmd. For better visualization, first change atom id from 1 to C by typing
sed "s/^1 /C /" movie.xyz > newmovie.xyz
Then load the newmovie.xyz into vmd and choose Graphics –> Representations and set Drawing Method to DynamicBonds. Create a second representation by clicking Create Rep and set the Drawing Method to VDW. Change the sphere scale to 0.3 and play the movie. You should observe the Stone-Wales transformation right before the end of the trajectory.
In this exercise we will run a VES simulation to fill the FES only up to a certain cutoff. This will be the first step in order to obtain kinetic information from biased simulations. In the previous section, we observed that a cutoff of 15 eV is too strong for our purpose. Change the cutoff energy from 15.0 to 6.0 eV by setting
BIAS_CUTOFF=6.0
and rerun the simulation from Exercise 1A. [Note: In practice one can use multiple walkers during the optimization by adding the flag MULTIPLE_WALKERS]
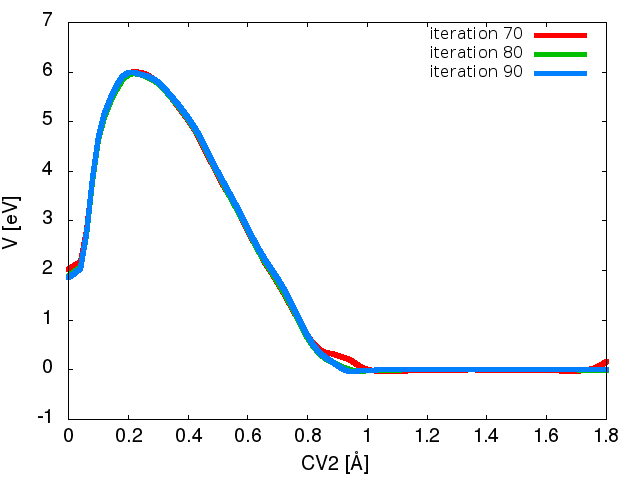
Plot some of the bias files (bias.variational.iter-n.data) that are printed during the simulation using gnuplot. At the end of the simulation, you should be able to reproduce something like Figure Figure1B. Is the bias converging? If so, how many iterations does it require to converge?
Figure Figure1B shows the bias potential after 70,80, and 90 iteration steps. Note that the bias has reached the cutoff and goes to zero at around 1 Angstrom.
In this exercise we will use the bias obtained above as a static umbrella potential. We will set up and run a new trajectory to measure the first passage time of escape from the well.
We can extract the coefficients that we need from the final iteration in Exercise-1B above.
tail -n 47 coeffs.dat > fixed-coeffs.dat
Now create a new directory from which you will run a new simulation and copy the necessary input files (including the fixed-coeffs.dat) into this directory. Modify the PLUMED file so that the optimized coefficients are read by the VES_LINEAR_EXPANSION
td_uniform: TD_UNIFORM VES_LINEAR_EXPANSION ... ARG=CV2 BASIS_FUNCTIONS=bf1 LABEL=variational TEMP=1700 BIAS_CUTOFF=6.0 BIAS_CUTOFF_FERMI_LAMBDA=10.0 TARGET_DISTRIBUTION=td_uniform COEFFS=fixed-coeffs.dat ... VES_LINEAR_EXPANSION
The final line specifies the coefficients to be read from a file.
Make sure to remove the lines for the stochastic optimization (OPT_AVERAGED_SGD) as we no longer wish to update the bias.
We will also perform metadynamics with an infrequent deposition stride to ensure that the trajectory does not get stuck in any regions where the bias potential is not fully converged The following implements metadynamics on both CV1 and CV2 with a deposition stride of 4000 steps and a hill height of 0.15 eV.
METAD ... ARG=CV1,CV2 SIGMA=0.2,0.2 HEIGHT=0.15 PACE=4000 LABEL=metad ... METAD
Again we will use the COMMITTOR to stop the trajectory after the transition.
COMMITTOR ARG=d1 BASIN_LL1=-2.0 BASIN_UL1=-1.0
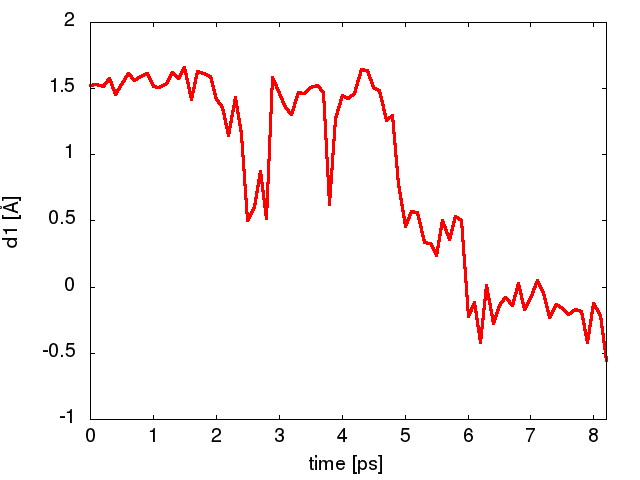
Now run a trajectory with the fixed bias. What is the time (biased) to escape? Plot the trajectory of the approximate reaction coordinate (column 4 in the COLVAR) in gnuplot. An example is shown in Figure Figure2.
Also look at the metadynamics bias in the column labeled metad.bias. How does the magnitude compare to the bias from VES in column variational.bias?
The crossing time for a single event doesn't tell us much because we don't have any statistics on the transition events. To obtain the mean first passage time, we have to repeat the calculation many times. To generate statistically independent samples, we have to change the seed for the random velocities that are generated in the LAMMPS input file. In a new directory, copy the necessary files and edit the following line in the input file
velocity all create 1700. 495920
Choose a different 6 digit random number and repeat Exercise 2. How does the escape time compare to what you obtained before? Repeat the procedure several times with different velocity seeds to get a distribution of first passage times. Make sure you launch each simulation from a separate directory and keep all COLVAR files as you will need them in the next section where we will analyze the transition times.
In the previous section you generated several trajectories with different first passage times. However, these times need to be re-weighted to correct for the bias potential. We can scale the time according to the hyperdynamics formula
\[ t^{*} = \Delta t_{MD} \sum_i^{n} e^{\beta V(s)} \]
Note that we need to add the total bias at each step, coming from both the VES bias and metadynamics. The python script time-reweighting.py will read the COLVAR from Exercise 2 and print the final reweighted time (in seconds). Open the script to make sure you understand how it works.
Run the script using
python time-reweighting.py
Note that the output first passage time is converted to seconds. What is the acceleration factor of our biased simulation? (i.e. the ratio of biased to unbiased transition times) The script also produces a time-reweighted trajectory COLVAR-RW for a specified CV (here we choose the approximate reaction coordinate, d1). Plot the reweighted COLVAR-RW in gnuplot and compare the original vs. time-reweighted trajectories. In particular, what effect does rescaling have on the time step?
Rerun the script for each of the trajectories you have run with the fixed bias and compute the mean first passage time from your data. The Stone-Wales transformation at 1700 K is estimated in fullerene to be ~10 days. How does your average time compare to this value?
The distribution of first passage times for an activated processes typically follows an exponential distribution. Instead of directly making a histogram of the first passage times, we can look at the cumulative distribution function which maps a value x to the fraction of values less than or equal to x. Since we are computing the cumulative distribution from a data set, this is called the empirical cumulative distribution (ECDF). On the other hand, the theoretical cumulative distribution (CDF) of an exponentially distributed random process is
\[ P(t) = 1-e^{-t/\tau} \]
where \(\tau\) is the mean first passage time.
In order to calculate the ECDF we need many trajectories. Several COLVAR files are included in the TRAJECTORIES-1700K directory. The script get-all-fpt.py is a modified version of time-reweighting.py and will calculate the first passage time (fpt) from all the simulation data and will output the times to a file fpt.dat. Run the script from the TRAJECTORIES-1700K directory
python get-all-fpt.py
You should obtain the output file fpt.dat which has a list of all the times. You can append your own values you obtained from Exercise 2 to the end of the list to increase the number of data points.
The script cdf-analysis.py will compute the ECDF and fit the distribution to the theoretical CDF. The script uses the statsmodels Python module. Run the script with
python cdf-analyysis.py
from the same directory where the fpt.dat file is located. The script prints both the mean first passage time of the data as well as the fit parameter \(\tau\). How do these two values compare?
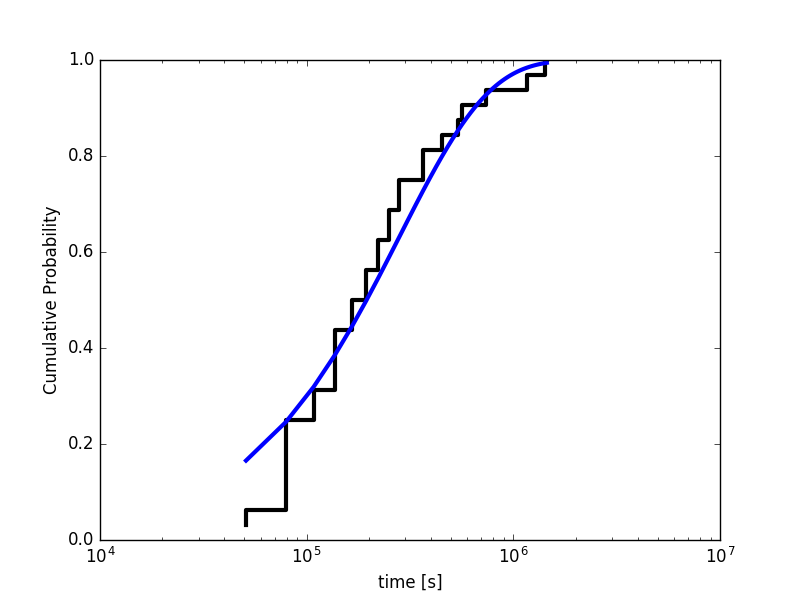
Figure Figure3 shows an example fit of the ECDF to the theoretical CDF for a Poisson process. To test the reliability of the fit, we can generate some data set according the theoretical CDF and perform a two-sample Kolmogorov-Smirnov (KS) test. The KS test provides the probability that the two sets of data are drawn from the same underlying distribution expressed in the so-called p-value. The null hypothesis is typically rejected for p-value < 0.05. The script cdf-analysis.py also performs the KS test and prints the p-value. What is the p-value we obtain from your dataset of transition times?